方格图
引子
由n*m的方格组成的二维平面，形成了一类常见而有趣味的问题。
方格可以蕴含着一个图或一种用于遍历的次序关系，可能作为思考的前提，也可能仅仅是可被忽略的问题背景。
2024icpc湖北省赛H
n*m的方格上有k(<10)个含🐟方格，1个方格最多含3条鱼，可以任选一个方格扔炸弹，炸出邻近方格的鱼，问最少炸几下能把🐟炸完。
在这里，问题的正解是DP，定义状态特征为每个方格还剩的鱼数，用状压表示，状态数是 $O(4^10=1e6)$的。记录每个状态所需最小炸鱼数，转移时枚举所有可能的方格($O(50)$)。
方格图的可能特征
有很多不同类别与角度，如
- 方格属于
- 行、列
- 对角线
- 九宫格 这是一类最基础的常识性的表示方式。对一个格子(x,y)，可以获知它的行为x，列为y，对角线表示为x+y(2-n+m), x-y(1-m - n-1)。若平面被划分为九宫格之类的结构，它所在的宫格坐标可记为((x-1)/k1,(y-1)/k2) (n/k1-1, m/k2-1)。
不同格子的关系
cf div4 F
200组测试，时限4s。
给出一组7*7方格，每个方格被涂了W,B两种颜色。可以选一些涂‘B’的格子涂成‘W’，问最少选几个修改，能使方格中不出现5个‘B’组成的‘X’？
发现可以把方格分成两组（25+24），只有每组内部可能组成‘X’形。 发现每组最多选4个即可消除所有的X。即搜索复杂度达到（C(25,4)+C(24,4)）*50左右
坐标
最普通的坐标就是(行数，列数)，注意从0还是1开始，x到底对应行还是列。 一个思维trick是坐标变换。
在坐标的意义下，方便考虑距离的概念。
距离
欧式距离
曼哈顿距离
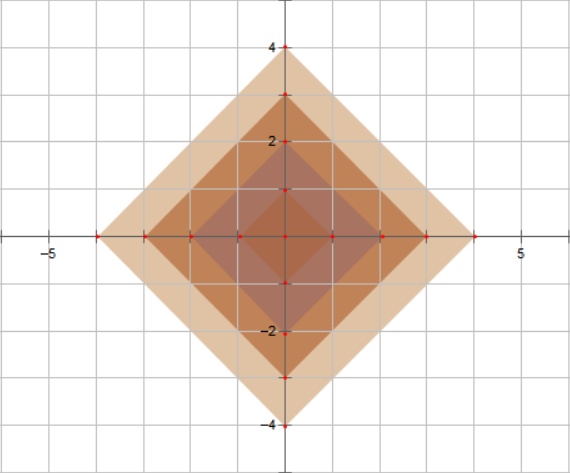
在国际象棋棋盘上，车从一个格子走到另一个格子的最短距离就是曼哈顿距离。 若网格图上的一个点只能到上下左右 4 个点，且到这 4 个点的距离都相同，则该网格图上两点的距离也为曼哈顿距离。
例：求点对曼哈顿距离最大值
二维平面上，共有n（<=5e4）个点，给出坐标，求曼哈顿距离最大的点对的最大值。 |x1-x2|+|y1-y2| = +-(x1-x2+y1-y2)或 = +-(x1-x2+y2-y1) 故只需分别求求所有点的(x+y)、(x-y) 最大、最小值，相减取最大值即可
切比雪夫距离
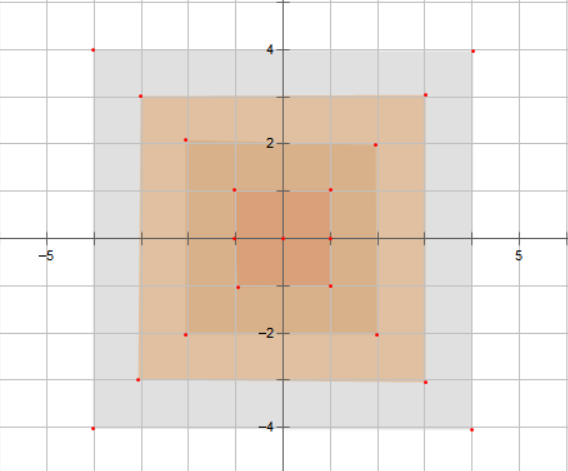在国际象棋棋盘上，国王从一个格子走到另一个格子的最短距离是切比雪夫距离。（从8个方向走）
若网格图上的一个点只能到周围 8 个点，且到这 8 个点的距离都相同，则该网格图上两点的距离也为切比雪夫距离。
例：abc351_e
有n（2e5）个点，定义点的距离是：从(x,y)格一次可以移动到 (𝑥+1,𝑦+1)，(𝑥+1,𝑦−1)， (𝑥−1,𝑦+1)， (𝑥−1,𝑦−1)，从A到B格的最少移动次数就是A到B的距离；若移不到就是0. 现在，求所有点的距离之和。
这里的距离定义和切比雪夫距离很像，但忽略了上下左右平移的情况。 得到如果横纵坐标之和奇偶性相同，距离大小和切比雪夫距离一致（可以列方程得到），否则就到不了，距离为0。
因此先分成两类讨论，再对每一类内部求所有点对切比雪夫距离和。
曼哈顿距离与切比雪夫距离互转
圆是由从圆心向各个固定XXX距离标示出来的点围成的区域。 曼哈顿距离和切比雪夫距离中的圆都是正方形 半径为r时，曼哈顿距离的圆边长√2r，切比雪夫距离的圆边长为2r，因此二维切比雪夫距离可视为等同于旋转且放大过的二维曼哈顿距离。 然而这种介于L1与L∞的相等关系不能延伸到更高的维度。
- 曼哈顿坐标系是通过切比雪夫坐标系旋转
45° 后，再缩小到原来的一半得到的。 - 将一个点(x,y)的坐标变为 (x+y,x-y)后，原坐标系中的曼哈顿距离等于新坐标系中的切比雪夫距离。
- 将一个点(x,y)的坐标变为 ((x+y)/2,(x-y)/2) 后，原坐标系中的切比雪夫距离等于新坐标系中的曼哈顿距离。 （考虑到精度问题，也可先转化为(x+y,x-y)，最后再/2）。
用场
曼哈顿距离只有求和以及取绝对值两种运算，把坐标排序后可以去掉绝对值的影响，进而用前缀和优化，可以把复杂度降为O(1)。 切比雪夫的两个坐标绝对值差取max，有时也有奇效。 需要视具体情况选择
例：续abc351_e
每一类内部求所有点对切比雪夫距离和。 先转化为曼哈顿距离，再对x和y分别排序后求曼哈顿距离和。 再/2即为切比雪夫距离和。
例： P4648 动物对数 曼哈顿转切比雪夫
要求处理空间维数为1，2，3的情况： 给出N个点(N<=1e5)，求曼哈顿距离小于等于D的点对数。 坐标是1-M间的整数
- 1维： M很大
- 2维： M<=7e4
- 3维： M<=75 曼哈顿距离转化为切比雪夫距离，则要求点对的x、y坐标差绝对值<=D。变成对2个坐标的限制。 那么可以先按顺序遍历x坐标，再处理y坐标。 分三种情况处理：
- 1维 逐点二分或滑动窗口找到和该点距离小于等于D的点数，减去这一点。最后ans/2，因为一个点对被两个点各计算一次。
- 2维 滑动窗口，维护x坐标满足要求的点的区间，把那些点的y坐标加入、删除。用树状数组统计满足要求的y坐标数量。
- 3维 对每个面分类讨论： 对每个面上的点，分别在每个面上计算二维曼哈顿距离限制，维护一遍滑动窗口。 注意到
- 不同的2个面里不一定会有x坐标满足条件的点对。
- 当且仅当在同一个面中维护滑动窗口时，需要考虑统计到点自身。 ps. 其实用二维前缀和统计切比雪夫距离内的正方形也可：毕竟M范围变得很小
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
typedef unsigned long long ull;
const int N = 7.5e4;
const int INF = 0x3f3f3f3f3f3f3f3f;
int n;
int m;
/// @brief ///////////
int tr[N * 3 + 10];
int lowbit(int x)
{
return x & (-x);
}
void update(int i, int x) // a[i]+=x;
{
// if(i==0)
// {
// tr[i]+=x;
// return;
// }
for (int j = i; j <= 3 * m + 5; j += lowbit(j))
{
tr[j] += x;
}
}
int query(int r) // a[0]+..+a[r]
{
if (r < 0)
return 0;
r = min(r, 3 * m + 5);
int sum = 0;
for (int i = r; i >= 1; i -= lowbit(i))
{
sum += tr[i];
}
return sum;
}
///////////
void solve()
{
int b;
cin >> b;
if (b == 1) ///
{
int n, d, m;
cin >> n >> d >> m;
vector<int> x(n + 1);
for (int i = 1; i <= n; ++i)
{
cin >> x[i];
}
sort(x.begin() + 1, x.end());
// for (int i = 1; i <= n; ++i)
// {
// cout << x[i] << " ";
// }
// cout << endl;
int ans = 0;
for (int i = 1; i <= n; ++i)
{
int l = i - 1, r = n + 1;
while (r - l > 1)
{
int mid = (l + r) >> 1;
if (x[mid] - x[i] <= d)
{
l = mid;
}
else
{
r = mid;
}
}
// r-l
ans += l - i;
// cout << l << " ";
l = 0, r = i + 1;
while (r - l > 1)
{
int mid = (l + r) >> 1;
if (x[i] - x[mid] <= d)
{
r = mid;
}
else
{
l = mid;
}
}
// cout << r << endl;
ans += i - r;
}
cout << ans / 2 << endl;
return;
}
if (b == 2)
{
int d;
cin >> n >> d >> m;
vector<array<int, 2>> p(n + 1);
for (int i = 1; i <= n; ++i)
{
int x, y;
cin >> x >> y;
p[i][0] = x + y + m + 5;
p[i][1] = x - y + m + 5;
}
sort(p.begin() + 1, p.end());
int l = 1, r = 1;
int ans = 0;
update(p[1][1], 1);
for (int i = 1; i <= n; ++i)
{
while (r + 1 <= n && p[r + 1][0] - p[i][0] <= d)
{
r++;
update(p[r][1], +1);
}
while (p[i][0] - p[l][0] > d)
{
update(p[l][1], -1);
l++;
}
// 滑动窗口
// l-r
ans += query(p[i][1] + d) - query(p[i][1] - d - 1) - 1;
}
cout << ans / 2 << endl;
return;
}
if (b == 3)
{
int d;
cin >> n >> d >> m;
int ans = 0;
vector<array<int, 2>> e[m + 1];
for (int i = 1; i <= n; ++i)
{
int x, y, z;
cin >> x >> y >> z;
e[z].emplace_back(array<int, 2>{x + y + m + 5, x - y + m + 5});
}
for (int i = 1; i <= m; ++i)
{
e[i].emplace_back(array<int, 2>{0, 0});
sort(e[i].begin(), e[i].end());
}
for (int z = 1; z <= m; ++z)
{
int n = e[z].size() - 1;
if (n == 0)
continue;
// cerr << "z1" << z << endl;
for (int z2 = max((int)1, z - d); z2 <= m && z2 <= z + d; ++z2)
{
// cerr << "z2" << z2 << endl;
int del = abs(z2 - z);
int nd = d - del;
int nm = e[z2].size() - 1;
if (nm == 0)
continue;
int l = 0;
int r = 0;
// cerr << "new d " << nd << endl;
// update(e[z2][1][1], +1);
for (int i = 1; i <= n; ++i)
{
// cerr << l << " " << r << endl;
while (r + 1 <= nm && e[z2][r + 1][0] - e[z][i][0] <= nd)
{
r++;
// cerr << r << " " << e[z2][r][0] << " " << e[z2][r][1] << endl;
update(e[z2][r][1], +1);
}
if (r > 0 && l == 0)
l = 1;
while (l != 0 && l <= r && e[z][i][0] - e[z2][l][0] > nd)
{
// cerr << l << endl;
update(e[z2][l][1], -1);
l++;
}
// 滑动窗口
// cerr << "l r " << l << " " << r << endl;
// l-r
ans += query(e[z][i][1] + nd) - query(e[z][i][1] - nd - 1);
if (z2 == z)
{
ans--;
}
}
while (l > 0 && l <= r)
{
update(e[z2][l][1], -1);
l++;
}
}
// cerr << "ok" << endl;
}
cout << ans / 2 << endl;
return;
}
}
signed main()
{
// cout.flags(ios::fixed); cout.precision(8);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int T = 1;
// cin >> T;
for (int i = 1; i <= T; ++i)
{
solve();
}
return 0;
}
/*
*/
例：P3964 松鼠聚会 切比雪夫转曼哈顿
1e5个点，其中必定存在1点使得到其它点的切比雪夫距离之和最小，求这个最小和。 转曼哈顿之后，分开计算x和y上的曼哈顿距离之和。
例：P2906 Cow Neighborhoods 曼哈顿转切比雪夫
有n(1e5)个点,坐标范围在1e9，给出C，规定点的曼哈顿距离小于等于C即连通，求有几个联通块和最大连通块的大小。
基本的想法是由并查集维护连通块。n^2 为了优化，维护连通块时，对每个点不O(n)地枚举另外所有点。 对点i来说，只需在满足$x_i-d \leq x_j \leq x_i+d , j\lt i$ 的点$i$中，找到y与$y_i$最接近的两点，若$y_i-d \leq y_j \leq y_i+d$，则连边。 需要证明正确性：
为什么不能用滑动窗口？？？
代码
移动
2022icpc南京A
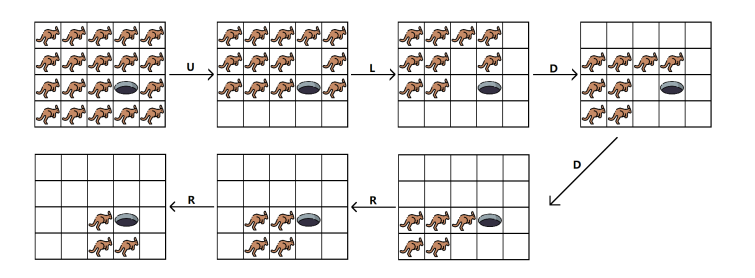n*m的方格，保证所有测试的n*m之和<1e6 。给出一个操作序列，在序列中如果袋鼠移出边界或落入洞中则消失，给出k作为最后剩余袋鼠数量，问多少个可能的点可以作洞的位置？
操作序列对应一个(delx,dely)的（去重）集合，记为s。
最后不溢出边界的袋鼠数量为r，区域形状是矩形，可计算在原位置中的坐标。
可以作洞的点，则是在s中恰有(r-k)个偏移量组合，让该点加上后能到达袋鼠矩阵中。让本矩阵在原区域中作多次区间加一得到每个点对应几个偏移量组合。
要点：
- 一个序列实质上对应的只是偏移量
- 得到的区域形状是矩形
南京2023A
发现连通块中，若有一个袋鼠是winner，其它所有袋鼠都是winner
